第一章 数字电路基础 目录
1.1 数字电路的基础知识
1.2 逻辑代数及运算规则
1.3 逻辑函数的表示法
1.4 逻辑函数的化简
以下内容为正文
1.1 数字电路的基础知识
1.1.1 数字信号和模拟信号
模拟电路与数字电路比较
1.电路的特点
在模拟电路中,晶体管一般工作在放大状态;在数字电路中,三极管工作在开关状态,即工作在饱和和截止状态。
2.研究的内容
模拟电路主要研究:输入、输出信号间的大小、相位关系、失真与否。模拟电路包括交直流放大器、滤波器、信号发生器等。
数字电路主要研究:电路输出、输入间的逻辑关系。主要的工具是逻辑代数,电路的功能用真值表、逻辑表达式及波形图表示。
1.1.3 数的进制与转换
一、十进制: Decimal System
每一位都有1、2、3、4、5、6、7、8、9、0
十个数码,位与位之间遵循逢十进一的规律。
一个十进制数数 N 可以表示成: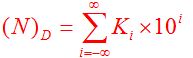
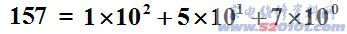
若在数字电路中采用十进制,必须要有十个电路状态与十个记数码相对应。这样将在技术上带来许多困难,而且很不经济。
二、二进制: Binary System
每一位只有两个数码 0或1,位与位之间遵循逢二进一的规律。
一个二进制数数 N 可以表示成: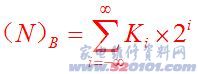
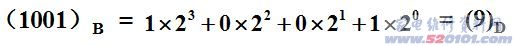
二进制的优点:电路中任何具有的两个不同稳定状态的元件都可用来表示一位二进制数,数码的存储和传输简单、可靠。
二进制的缺点:位数较多,不便于读数;不合人们的习惯,输入时将十进制转换成二进制,运算结果输出时再转换成十进制数。
三、十六进制和八进制
1. 十六进制与二进制之间的转换。
说明:十六进制的一位对应二进制的四位。
1.1.4常用的二---- 十进制编码
二进制编码: 将二进制数字的符号“0”和“1”按一定的规律排列,并赋予每一种排列一个固定的含义,这样的过程就叫二进制编码。
这样得到的每一个有固定含义的排列就称为一个二进制代码。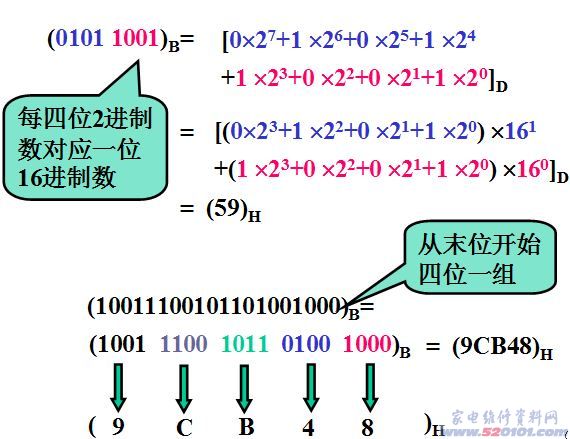
四、十进制与二进制之间的转换
十进制与二进制之间的转换方法:可以用二除十进制数,余数是二进制数的第0位K0,然后依次用二除所得的商,余数依次是第1位K1 、第2位K2 、……。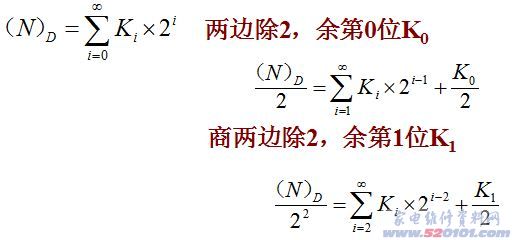
例:十进制数25转换成二进制数的转换过程: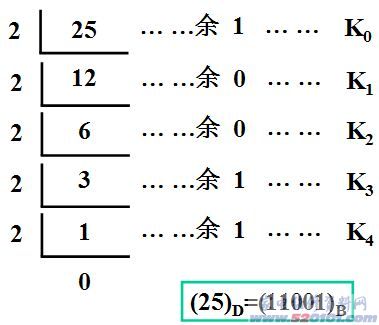
由于人们生活中习惯采用的是十进制,而数字电路便于采用的是二进制,这自然就提出了如何用二进制编码来表示十进制数的问题,即二---- 十进制编码的问题。
BCD-Binary Coded Decimal (二进制编码的十进制代码)
BCD码用四位二进制数表示0~9十个数码。四位二进制数最多可以表示16个字符,因此,从16种表示中选十个来表示0~9十个字符,可以有多种情况。不同的表示法便形成了一种编码。这里主要介绍: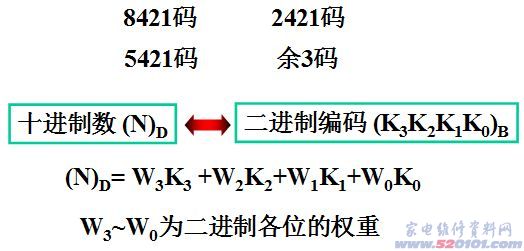
所谓的8421码,就是指各位的权重是8、4、2、1。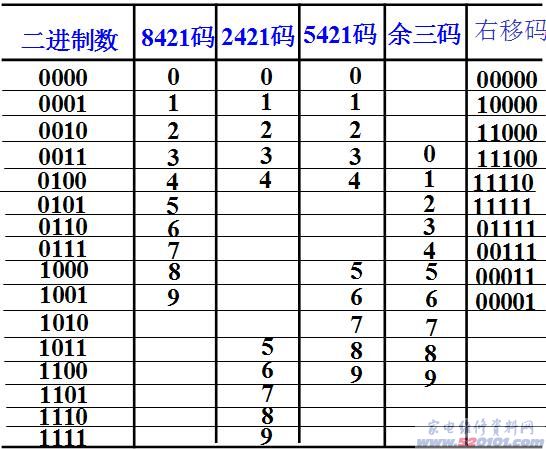
§1.2 逻辑代数及运算规则
1.2.1 基本逻辑关系与逻辑代数
数字电路要研究的是电路的输入输出之间的因果关系,也就是逻辑关系,所以数字电路又称逻辑电路,相应的研究工具是逻辑代数(逻辑代数是19世纪中叶英国数学家布尔首先提出的,所以又叫布尔代数)。
逻辑关系是如何来表述的呢?
如果决定某一件事F发生或成立与否的条件
有多个,分别用A、B、C表示,并规定:
F=“1” 代表事件发生(或成立),
F=“0” 代表事件不发生(或不成立);
A=B=C=“1” 代表条件具备,
A=B=C=“0 ”代表条件不具备;
那麽F与ABC之间就有以下三种基本的逻辑关:
1.“与”逻辑
A、B、C都具备时,事件F才发生。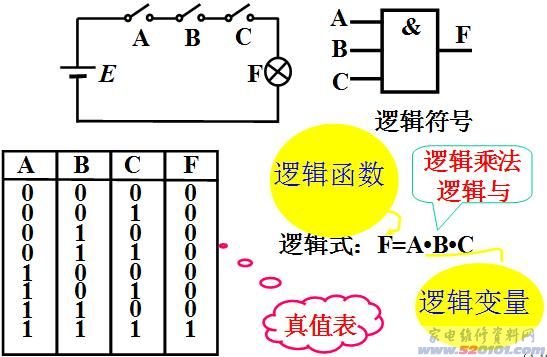
3. “非”逻辑
A具备时 ,事件F不发生;A不具备时,事件F发生。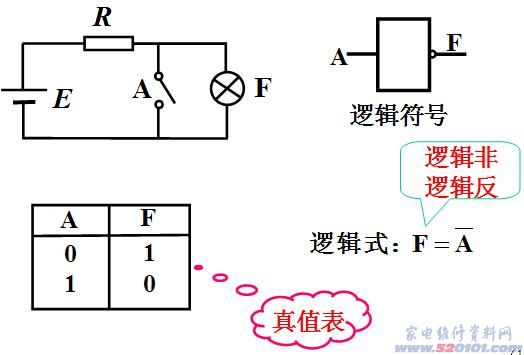
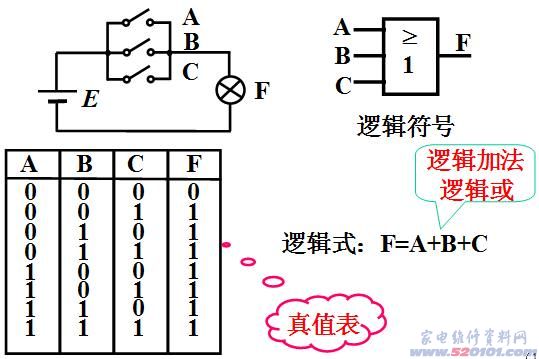
4. 几种常用的逻辑关系逻辑
“与”、“或”、“非”是三种基本的逻辑关系,任何其它的逻辑关系都是在此基础上发展的。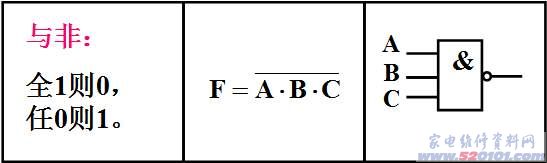

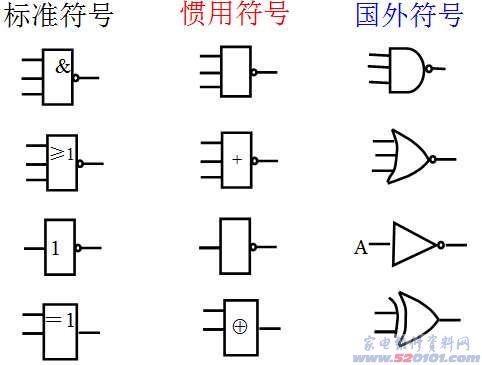
5. 几种基本的逻辑运算
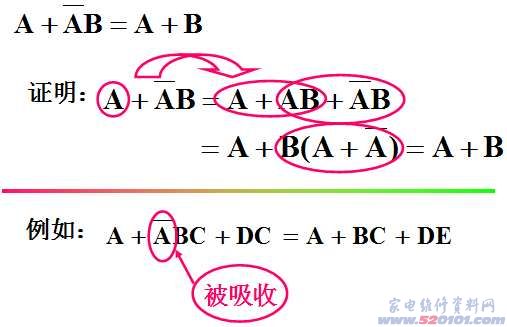
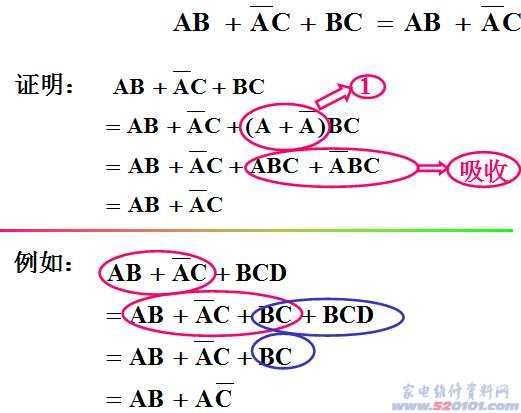
从三种基本的逻辑关系,我们可以得到以下逻辑运算:
0• 0=0 • 1=1 • 0=0
1 • 1=1
0+0=0
0+1=1+0=1+1=1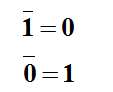
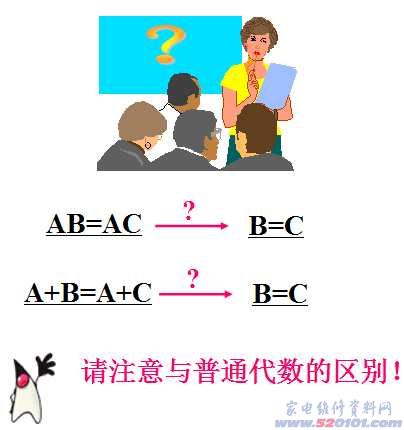
注意:
A+B=A+C 未必有B=C
A•B = A•C 未必有B=C
逻辑代数中没有减法与除法。
§1.3 逻辑函数的表示法
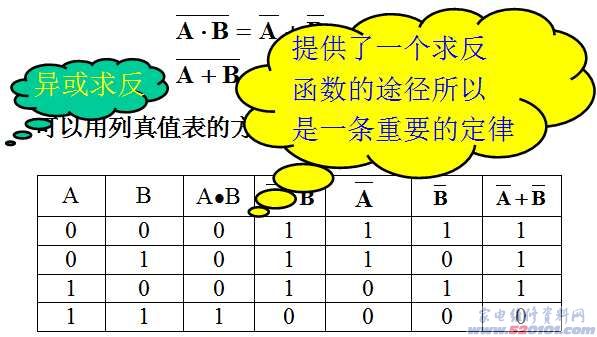
1.3.1 真值表
将输入、输出的所有可能状态一一对应地列出。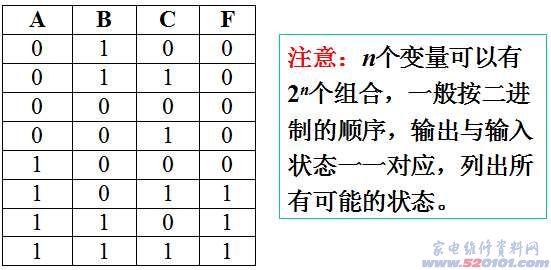
1.3.2 逻辑函数式
逻辑代数式:把逻辑函数的输入、输出关系写成与、或、非等逻辑运算的组合式。也称为逻辑函数式,通常采用“与或”的形式。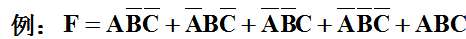
最小项:若表达式中的乘积包含了所有变量的原变量或反变量,则这一项称为最小项。
上例中每一项都是最小项。
逻辑相邻:若两个最小项只有一个变量以原、反区别,则称它们逻辑相邻。 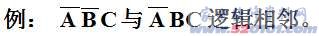
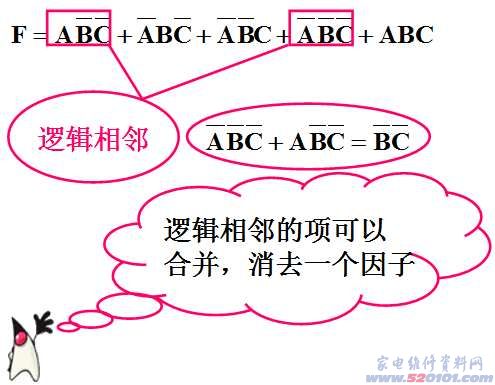
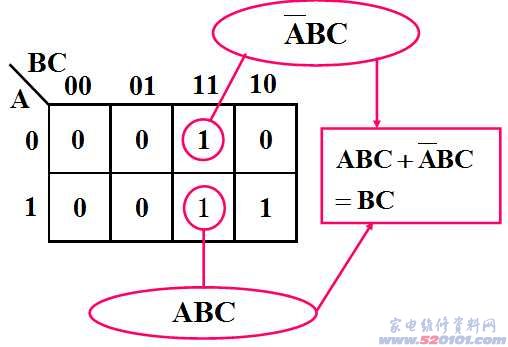
1.3.3 卡诺图
卡诺图的构成:将n个输入变量的全部最小项用小方块阵列图表示,并且将逻辑相临的最小项放在相临的几何位置上,所得到的阵列图就是n变量的卡诺图。
卡诺图的每一个方块(最小项)代表一种输入组合,并且把对应的输入组合注明在阵列图的上方和左方。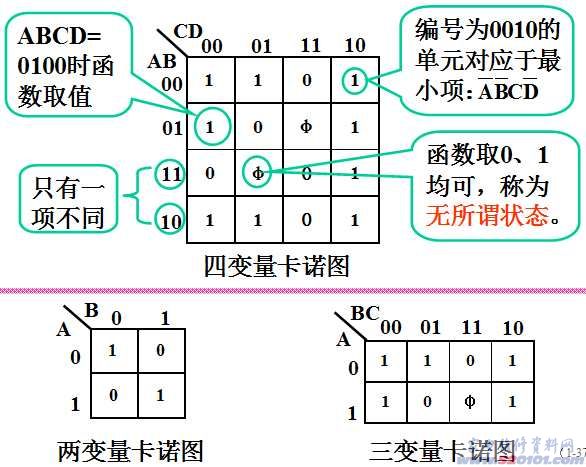
有时为了方便,用二进制对应的十进制表示单元格的编号。单元格的值用函数式表示。
1.3.4 逻辑图
把相应的逻辑关系用逻辑符号和连线表示出来,就构成了逻辑图。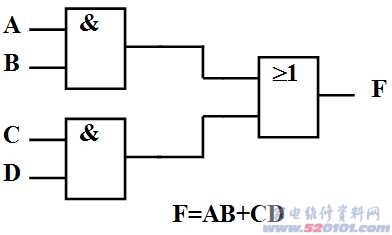
化简过程: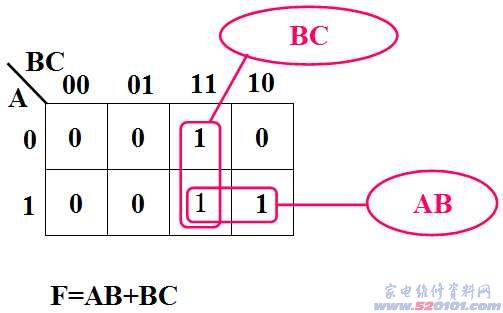
利用卡诺图化简的规则
1. 相邻单元的个数是2N个,并组成矩形时,可以合并。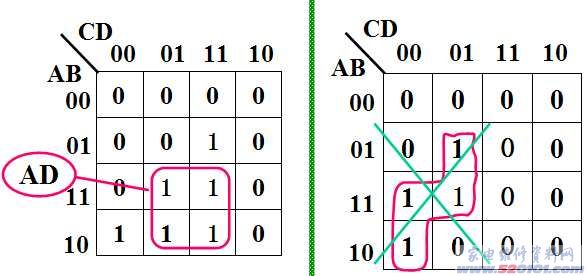
2. 先找面积尽量大的组合进行化简,可以减少每项的因子数。
3. 各最小项可以重复使用。
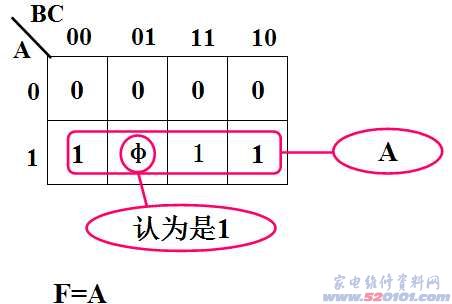
4. 注意利用无所谓状态,可以使结果大大简化。
5. 所有的1都被圈过后,化简结束。
6. 化简后的逻辑式是各化简项的逻辑和。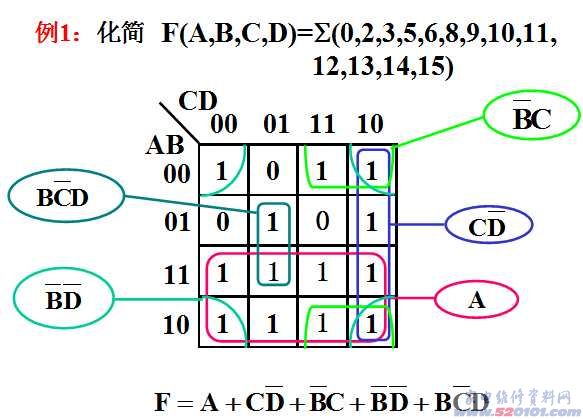
例2:化简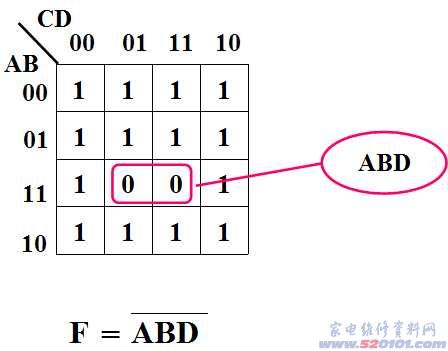
例3:已知真值表如图,用卡诺图化简。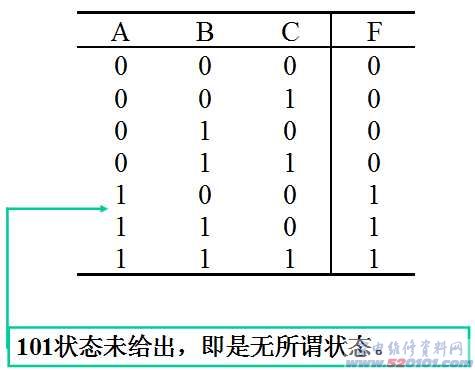
第一课课程完结,未完,待续...

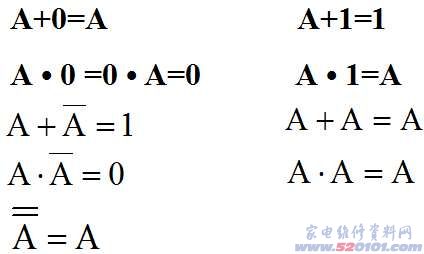




网友评论