首先找出振荡器的三个组成部分,即放大环节、反馈网络和选频网络。一般怍为放大环节的有源器件可以是晶体管、场效应管、差分对管、线性集成电路、电子管等;作为反馈网络可以是变压器、耦合电路、电感分压电路、电容分压电路等;作为选频网络的可以是Lc谐振回路、RC移相(或选频)电路、石英晶体谐振器等。
其次检查放大环节的偏置电路和静态工作点是否能使放大器正常工作。可画出直流等效电路看静态工作点是否合适。对于晶体管来说一般静态工作点选择靠近截止区,然后分析是否满足相位和振幅条件。不同振荡电路,其相位和振幅条件不同。一般振幅条件较易满足。相位条件可以用瞬时极性法去分析。不同电路具体方法亦不完全相同,实际上就是判断通过反馈网络是否引入了正反馈。我们以最常见的三点式振荡器为例分析如何判断电路是否能振荡。 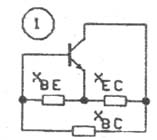
图1为三点式振荡器的交流等效电路。如XBE与XEC的电抗性质相同,XBC与之电抗性质相反,则这时的电路满足相位平衡条件。如XBE、XEC显感性则为电感三点式振荡器,如显容性则为电容三点式振荡器。实际分析画出交流等效电路时要特别注意电路中的电容和电感的参数不同所起的作用不同,具体要视振荡电路的频率而定。耦合电容和旁路电容比振荡回路的电容容量大,应看成短路,振荡回路的电容和电感应照原位置画出。与振荡回路并联的电阻一般讲只改变电路的品质因数和振荡频率以及影响主回路的增益,它不影响相位条件;与振荡回路电容、电感串联的电阻将使电路损耗增大,不容易振荡,即振荡条件不易满足,有它还将产生桕移,使相位条件也不易满足。一般讲,并联电阻的阻值越大,串联的电阻阻值越小,对电路的影响就越小。 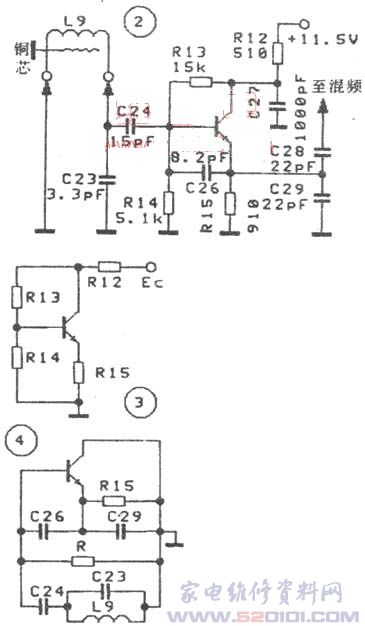
图2为某电视机的振荡电路。首先找出振荡电路的三个组成部分。放大环节由三极管组成,反馈网络由C26、C29分压组成,选频网络由C26、C29、C23、C24和L9等组成。其次画出直流等效电路如图3所示。由R12、R13、R14、R15组成三极管的静态偏置电路,R13构成电压并联负反馈,R15构成串联负反馈来稳定静态工作点。然后再画出交流等效电路如图4,C27看成短路,C28为耦合电容可不画,其它照画即可。由图4可见,与发射极相连的为两个电容器C26、C29,连在BC两极的为C24、C23、L9组成呈感性的电路,则满足电容三点式振荡的相位条件,而R15、R(为R13、R14的并联值)与振荡同路并联不影响振荡。参数选择要考虑振荡频率、变化范围、稳定性,振荡频率取决于C23、C24、C26、C29、L9,调节L9中的铜芯可调节振荡频率。旁路电容C27使之成为共集电极振荡电路,同时与R12组成电源滤波电路,R15为负载电阻,C28为耦台电容将本振信号注入混频器。三极管一般选低噪声管。图4为西勒式电容三点式振荡器,如去掉C23就变成卡拉泼式电容三点式振荡器,再去掉C24就变成普通的电容三点式振荡器。
三点式振荡器是反馈式高频振荡器的一种类型。它能否振荡最重要的是应判别其电路是否满足相位平衡条件,即反馈电压的相位是否与原输入回路电压相位一致。 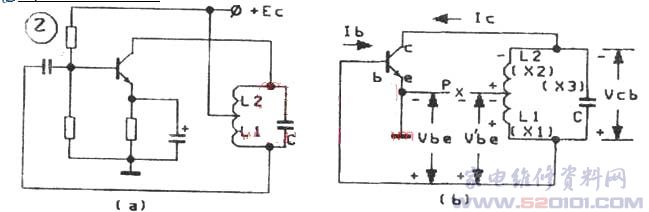
图1(a)为共射极电容三点式振荡电路,图1(b)为其交流通路。
电路振荡时,谐振回路处在谐振状态,其总电抗为零,故其阻抗呈现纯电阻。将谐振回路的损耗忽略,则接到晶体管e、b、c三个电极之间的元件均为电抗元件。令:接在输入回路b、c之间电容C1的电抗为x1;接在输出回路c、e间电容c2的电抗为x2;接在反馈回路c、b间电感L的电抗为X3。
判别方法是:预先假定一个瞬时变化的电压作用于输人端,再分析信号的传输及反馈过程,看反馈电压是否与假定的输入电压极性一致。在图1(b)中,可先将图中P点断开,设想在b、e间加入信号电压Vbe,极性正负如图,则将引起Ib流向基极,随之Ic流向集电极,在谐振回路上引起电压降Vcb,其极性为下正上负。因x1、X2为同类容性电抗,故c1、C2上的分压极性也都是下正上负。c1上的分压又是反馈电压V’be,因此可看出其极性与Vbe的一致,满足了相位平衡条件,只要电路再满足振幅平衡条件(AF≥1),即可产生振荡。在实用上,只要直流偏置正常,晶体管在高频时的β值足够大,并且C2/c1值选取适当,此电路是很容易振荡的。 
若将图1中电容与电感互换,即可构成电感三点式振荡电路(图2a)。用同法在其交流通路中(图2b)也可判定它是满足相位平衡条件的。
由此可得到共射极三点式振荡电路满足相位平衡条件的简单判别准则为:
1.x1与X2必须为同类电抗元件;2.x1、X2与x3必须为异类电抗元件。
简言之,“1、2相同3相反”,这一结论对判别三点式振荡电路的相位条件很有用。例如,图3的两振荡电路用此准则来判别,就可很快知道它们因不满足相位平衡条件而不能振荡。
网友评论